2025程序设计天梯赛补题报告
仅包含L1 L2
L1-6 这不是字符串题
题目描述
因为每年天梯赛字符串题的解答率都不尽如人意,因此出题组从几年前开始决定:每年的天梯赛的 15 分一定会有一道字符串题,另外一道则一定不是字符串题。
小特现在有 N 个正整数 $A_i$,不知道为什么,小特打算”动”一下这些数字。具体而言,她希望做 M 次操作,每次是以下三种操作之一:
- 在当前正整数序列里查找给定的连续正整数序列是否存在,如存在,则将其替换成另外一个正整数序列;
- 对于当前整个正整数序列,如果相邻之间的数字和为偶数,则在它们中间插入它们的平均数;
- 翻转当前正整数序列指定下标之间的一段数字。这里的翻转指的是对于一段数字序列 $A_i$,$A_{i+1}$,…,$A_{j-1}$,$A_j$,将其变为 $A_j$,$A_{j-1}$,…,$A_{i+1}$,$A_i$。
请你输出按输入顺序依次完成若干次操作后的结果。
求解思路
可选2种数据结构维护:
- vector
- string
这里挺有意思的,因为数值大小是1-26所以可以用字符来代替数字
以下是vector的2个在本题涉及的方法
insert
插入单个元素:
1
| iterator insert(iterator pos, const T& value);
|
pos:插入位置的迭代器。value:要插入的元素。
插入多个相同元素:
1
| iterator insert(iterator pos, size_type count, const T& value);
|
pos:插入位置的迭代器。count:插入元素的数量。value:要插入的元素。
插入范围内的元素:
1
2
| template<class InputIt>
iterator insert(iterator pos, InputIt first, InputIt last);
|
pos:插入位置的迭代器。first:要插入的起始迭代器。last:要插入的结束迭代器。
插入初始化列表中的元素:
1
| iterator insert(iterator pos, std::initializer_list<T> ilist);
|
pos:插入位置的迭代器。ilist:包含要插入元素的初始化列表。
erase
删除单个元素:
1
| iterator erase(iterator pos);
|
删除范围内的元素:
1
| iterator erase(iterator first, iterator last);
|
first:要删除的起始迭代器。last:要删除的结束迭代器。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, m;
vector<LL> a;
int main() {
cin >> n >> m;
for (LL i = 0; i < n; i++) {
LL t;
cin >> t;
a.push_back(t);
}
while (m--) {
LL k;
cin >> k;
if (k == 1) {
LL L1, L2;
cin >> L1;
vector<LL> a1, a2;
for (LL i = 0; i < L1; i++) {
LL t;
cin >> t;
a1.push_back(t);
}
cin >> L2;
for (LL i = 0; i < L2; i++) {
LL t;
cin >> t;
a2.push_back(t);
}
for (LL i = 0; i < a.size() - L1 + 1; i++) {
LL flag = 1;
for (LL j = 0, now = i; j < a1.size(); j++, now ++) {
if (a[now] != a1[j]) {
flag = 0;
break;
}
}
if (flag) {
a.erase(a.begin() + i, a.begin() + i + L1);
a.insert(a.begin() + i, a2.begin(), a2.end());
break;
}
}
}
else if (k == 2) {
vector<LL> t;
for (LL i = 0; i <a.size() - 1; i++) {
t.push_back(a[i]);
if ((a[i] + a[i + 1]) % 2 == 0) t.push_back((a[i] + a[i + 1]) / 2);
}
t.push_back(a.back());
a= t;
}
else if (k == 3) {
LL l, r;
cin >> l >> r;
l--, r--;
reverse(a.begin() + l, a.begin() + r + 1);
}
}
for (LL i = 0; i < a.size(); i++) {
cout << a[i];
if (i != a.size() - 1) cout << " ";
}
return 0;
}
|
L1-7 大幂数
题目描述
如果一个正整数可以表示为从 1 开始的连续自然数的非 0 幂次和,就称之为“大幂数”。例如 2025 就是一个大幂数,因为 2025=1^3^+2^3^+3^3^+4^3^+5^3^+6^3^+7^3^+8^3^+9^3^。本题就请你判断一个给定的数字 n 是否大幂数,如果是,就输出其幂次和。
另一方面,大幂数的幂次和表示可能是不唯一的,例如 91 可以表示为 9^1^=1^1^+2^1^+3^1^+4^1^+5^1^+6^1^+7^1^+8^1^+9^1^+10^1^+11^1^+12^1^+13^1^,同时也可以表示为 9^1^=1^2^+2^2^+3^2^+4^2^+5^2^+6^2^,这时你只需要输出幂次最大的那个和即可。
求解思路
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5;
LL n;
LL a[N][40];
int main() {
cin >> n;
if (n == 1) {
cout << "1^1";
return 0;
}
for (LL j = 1; j <= 31; j++) {
for (LL i = 1; i < N; i++) {
a[i][j] = a[i - 1][j] + pow(i, j);
}
}
for (LL j = 31; j >= 1; j--) {
for (LL i = 1; i < N; i++) {
if (a[i][j] == n) {
for (LL x = 1; x <= i; x++) {
if (x != 1) cout << "+";
cout << x << "^" << j;
}
return 0;
}
else if (a[i][j] > n) break;
}
}
cout << "Impossible for " << n << ".";
return 0;
}
|
L2-1 算式拆解
题目描述
括号用于改变算式中部分计算的默认优先级,例如 2+3×4=14,因为乘法优先级高于加法;但 (2+3)×4=20,因为括号的存在使得加法先于乘法被执行。本题请你将带括号的算式进行拆解,按执行顺序列出各种操作。
注意:题目只考虑 +、-、*、/ 四种操作,且输入保证每个操作及其对应的两个操作对象都被一对圆括号 () 括住,即算式的通用格式为 (对象 操作 对象),其中 对象 可以是数字,也可以是另一个算式。
求解思路
这题非常眼熟,在学习stack的时候就学过类似的。反正其实就是一道简单的stack题,当时比赛没写出来还是因为思维不够清晰,应该多训练,这样以后就能对题目的意思更加敏感,就不会写不出。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
stack<char> s;
int main() {
string str;
getline(cin, str);
for (char c : str) {
if (c == ')') {
string t;
while (s.top() != '(') {
t += s.top();
s.pop();
}
s.pop();
reverse(t.begin(), t.end());
cout << t << endl;
}
else s.push(c);
}
return 0;
}
|
L2-2 三点共线
题目描述
给定平面上 n 个点的坐标 ($x_i$,$y_i$)(i=1,⋯,n),其中 y 坐标只能是 0、1 或 2,是否存在三个不同的点位于一条非水平的直线上?
本题就请你找出所有共线的解。
求解思路
这题直接简单模拟一下是o(n^3^),n<=5×10^4^,时间限制2s,1s大约可以处理10^8^,那样肯定超时,需要优化到o(n^3^),那就需要想到把y=2的点换一个情况存,不能在直接vector一个个存了。那就直接开个坐标数组记录一下y=2时在某个x的情况下有没有点存在即可,因为我们这个点的x坐标是直接算出来的,不需要遍历,所以这样存就是最快的。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
struct coord {
LL x, y;
};
vector<LL> a0, a1;
bool a2[3000100];
LL ans0 = 0, ans1 = 0, ans2 = 0, flag = 0;
LL n;
LL N = 1e6;
int main() {
cin >> n;
for (LL i = 0; i < n; i++) {
LL x, y;
cin >> x >> y;
if (y == 0) a0.push_back(x);
else if (y == 1) a1.push_back(x);
else if (y == 2) a2[x + N] = 1;
}
sort(a0.begin(), a0.end()), sort(a1.begin(), a1.end());
LL qian_x1, flag1 = 0;
for (LL i = 0; i < a1.size(); i++) {
LL x1 = a1[i];
if (i > 0 && a1[i-1] == x1) continue;
for (LL j = 0; j < a0.size(); j++) {
LL x0 = a0[j];
if (j > 0 && a0[j-1] == x0) continue;
LL x2 = x1 + (x1 - x0);
if (x2 >= -N && x2 <= N && a2[x2 + N]) {
flag = 1;
printf("[%lld, 0] [%lld, 1] [%lld, 2]\n", x0, x1, x2);
}
}
}
if (!flag) cout << -1;
return 0;
}
|
L2-3 胖达的山头
题目描述
胖达是大熊猫的昵称。上图是著名的“西直门三太子”萌兰的一字马。
一只成年大熊猫需要有自己独立的生活区域,如果两只成年大熊猫在同一时间进入同一片区域,很可能会发生打斗事件。
大熊猫保护中心计划将保护区划分成若干座山头,让胖达们都过上没有冲突的安逸生活。当然如果为每位胖达分配一个山头是最理想的,但中心计划安置数十万只胖达 —— 这是个长远计划(截至2024年,世界上共有近 1900 只大熊猫),而保护区面积有限,这样做会使得每个山头面积过于局促。于是中心负责人找到了你,带着所有胖达的活跃时间表,请你帮助他们计算一下,如果让所有活跃时间段内的胖达都位于不同的山头,最少需要建设多少个山头?
求解思路
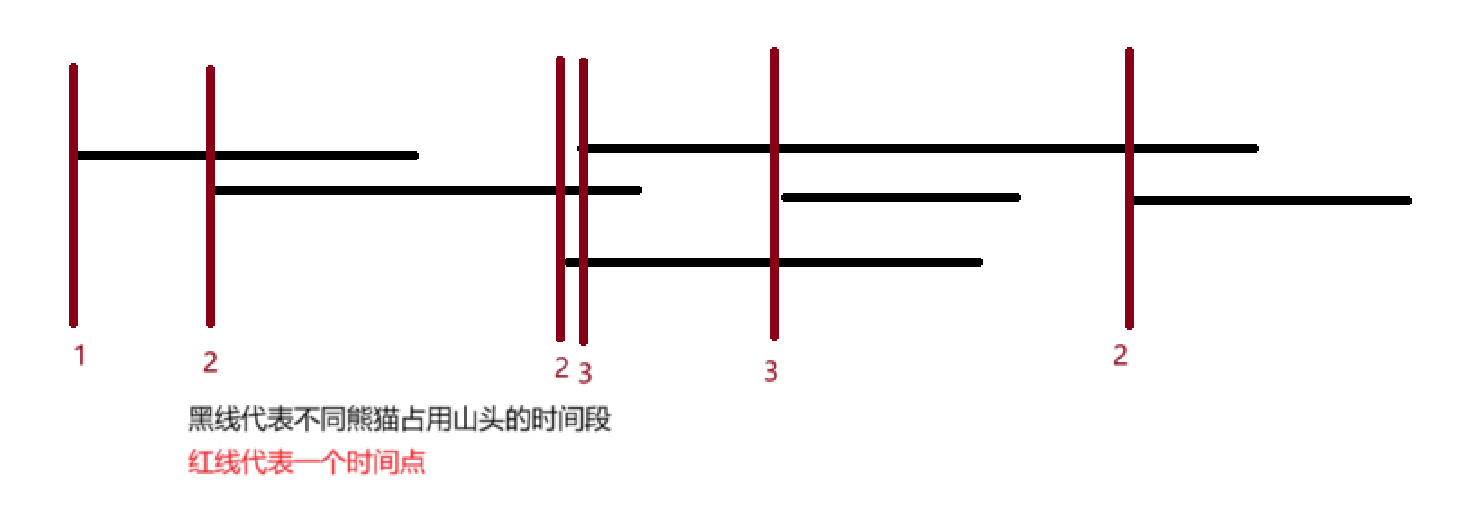
这题模拟一下就是以时间为坐标,求占用最多占用山头的时候的占用山头数量。然后就可以画出上面的黑线,然后思考怎么求答案呢?那就是只要在每次有新的熊猫占用山头的时候算一下占用数,然后把全部的这个数值取最大值即可(贪心)。
然后怎么维护时间的区间呢?然后就看一下数据大小,时间从从 00:00:00 到 23:59:59,那其实每一个时间点(按秒算)都可以算一个坐标了,一个数组就能存下,nice!再然后当然不能直接一个一个的点的维护区间了,不然嘎嘎超时,理所应当想到区间用差分,就可以愉快的敲代码了。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PII;
vector<PII> a;
LL coord[100000];
LL n, res = 0;
void insert(LL num, LL l, LL r) {
coord[l] += num, coord[r + 1] -= num;
}
int main() {
cin >> n;
for (LL i = 0; i < n; i++) {
LL h1, m1, s1, h2, m2, s2;
scanf("%lld:%lld:%lld %lld:%lld:%lld", &h1, &m1, &s1, &h2, &m2, &s2);
LL begin = h1 * 3600 + m1 * 60 + s1, end = h2 * 3600 + m2 * 60 + s2;
a.push_back({begin, end});
}
sort(a.begin(), a.end());
for (auto qj : a) {
LL begin = qj.first, end = qj.second;
insert(1, begin, end);
}
for (LL i = 1; i < 100000; i++) {
coord[i] += coord[i - 1];
}
for (auto qj : a) {
LL begin = qj.first;
res = max(res, coord[begin]);
}
cout << res;
return 0;
}
|
L2-4 被n整除的n位数
题目描述
“被 n 整除的 n 位数”是这样定义的:记这个 n 位数为 $a_n$⋯$a_2$$a_1$。首先 $a_n$ 不为 0。从 $a_n$ 开始从左到右扫描每一位数字,前 1 位数(即 $a_n$)能被 1 整除,前 2 位数 $a_n$$a_{n-1}$ 能被 2 整除,以此类推…… 即前 i 位数能被 i 整除(i=1,⋯,n)。
例如 34285 这个 5 位数,其前 1 位数 3 能被 1 整除;前 2 位数 34 能被 2 整除;前 3 位数 342 能被 3 整除;前 4 位数 3428 能被 4 整除;前 5 位数 34285 能被 5 整除。所以 34285 是能被 5 整除的 5 位数。
本题就请你对任一给定的 n,求出给定区间内被 n 整除的 n 位数。
友情提示:被偶数整除的数字一定以偶数结尾;被 5 整除的数字一定以 5 或 0 结尾;被 10 整除的数字一定以 0 结尾。
求解思路
这题可以看到这个数字可以是从高位开始一位一位生成的,可以用dfs。然后看到题目中的一堆条件就知道肯定可以剪枝,这样优化后就能够过题了。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
long long a, b;
vector<long long> results;
void dfs(int depth, long long current) {
if (depth == n) {
if (a <= current && current <= b) {
results.push_back(current);
}
return;
}
int start_digit = (depth == 0) ? 1 : 0;
for (int digit = start_digit; digit <= 9; digit++) {
long long new_num = current * 10 + digit;
long long min_possible = new_num * pow(10, n - depth - 1);
if (min_possible > b) {
break;
}
long long max_possible = min_possible + pow(10, n - depth - 1) - 1;
if (max_possible < a) {
continue;
}
if ((depth + 1) > 0 && new_num % (depth + 1) != 0) {
continue;
}
if ((depth + 1) % 2 == 0 && digit % 2 != 0) {
continue;
}
if ((depth + 1) % 5 == 0 && digit != 0 && digit != 5) {
continue;
}
if ((depth + 1) % 10 == 0 && digit != 0) {
continue;
}
dfs(depth + 1, new_num);
}
}
int main() {
cin >> n >> a >> b;
long long min_n_digit = pow(10, n-1);
long long max_n_digit = pow(10, n) - 1;
a = max(a, min_n_digit);
b = min(b, max_n_digit);
if (a > b) {
cout << "No Solution" << endl;
return 0;
}
dfs(0, 0);
if (results.empty()) {
cout << "No Solution" << endl;
} else {
for (long long result : results) {
cout << result << endl;
}
}
return 0;
}
|



.jpg)
.jpg)
.jpg)
.jpg)