二分法的几种实现
二分法的几种实现
前言
二分法的实现方式有很多种,在这里整理几种方法,他们各有优缺点,可以从上到下逐渐深入学习。
二分法说明
二分分为二分查找和二分答案:
- 二分查找:
- 用途:在一个有序数组中查找特定元素的位置。
- 原理:通过不断将搜索范围减半,快速找到目标元素或确定其不存在。
- 适用场景:需要在已排序的集合中查找某个具体元素。
- 二分答案:
- 用途:解决一些优化问题,通常用于确定满足某种条件的最优解的范围(如最大值或最小值)。
- 原理:通过二分法在一个范围内查找使某个条件成立的极限值。
- 适用场景:问题的解具有单调性,通常需要在一个连续的数值范围中找到最优解。
两者的主要区别在于应用场景:二分查找用于查找具体值,而二分答案用于查找满足某种条件的最优解。
二分查找有几种查找类型:
- 找到”=x”的元素
- 第一个
- 最后一个
还有
- 找到第一个”>=i”的元素
- 找到最后一个”<i”的元素
- 找到第一个”>i”的元素
- 找到最后一个”<=i”的元素
其中二分还分为整数二分和实数二分,实数二分在最后提及。
二分实现
以下默认定义好了数列a,数列下标从1开始,元素个数(不包括0)n,且数列为升序。
以下l + (r - l) / 2其实就是(l + r) / 2,这样写是为了避免溢出,同时如果不考虑溢出问题还可以写成l + r >> 1。
虽然以下代码都没开long long,但是为了保险起见,在写题的时候最好开一下。
第一种
1 | int find(int x) { |
这是最好理解的算法,但是其并不完美,其只能实现第一种查找,并且不能确定第一个或者最后一个。
第二种
1 | int find(int x) { |
这个算法可以实现上面五种查找,这里的代码演示的是第一种查找,并且查找的是第一个出现的元素,如果想要查找最后的就把判断语句修改为
1 | if (a[mid] <= x) l = mid + 1; |
并把下面两处的l修改为r - 1。
反正就是想找靠左的就用l去找,靠右的就用r - 1去找。
这个算法同时还可以实现其他四种查找,反正就是把判断条件写好,并把最后判断数据是否相同才返回的代码删除或者写好就行。
这个算法其实难度较大,不建议平时使用,因为需要处理好边界问题、循环判断问题等琐碎细节。写这个算法的时候需要特别注意是小于还是小于或等于,有没有加1、减1等细节。
第三种
这个方法使用起来和第四种效果差不多,但是还是比第四种难写,可以直接看第四种
针对第一种查找的实现:
1 | int find(int x) { |
这个算法实现了查找最先或者最后出现的元素,如果想要查找最后出现的就把判断语句中的>=改为>。
针对后四种查找和二分答案的实现:
1 | int find() { |
判断函数 p 按照题目要求另外写即可。
以上代码实现的是某种判断条件下寻找符合条件的最左边的元素(同时要判断函数p配合),如果要找最右边的就需要把r和l的赋值语句调换,并在判断函数p中修改逻辑。
反正想要实现另外四种查找的话,就要按照实际情况去写好判断函数p和r跟l赋值语句的顺序。
这个方法相较前面的方法更方便记忆,只需要想清楚答案是否需要更新(是否记下ans)和(可能的)答案在哪一侧(改l还是r)即可。
第四种
针对第一种查找的实现:
1 | int find(int x) { |
针对后四种查找和二分答案的实现:
1 | int find() { |
该算法非常好理解和记忆,只要分左边的蓝区和右边的红区,然后不断二分查找直到全部蓝红分区完成,再按照实际情况返回l或者r即可。
原理和更深层教学请看VCR。
放个后四种查找的案例
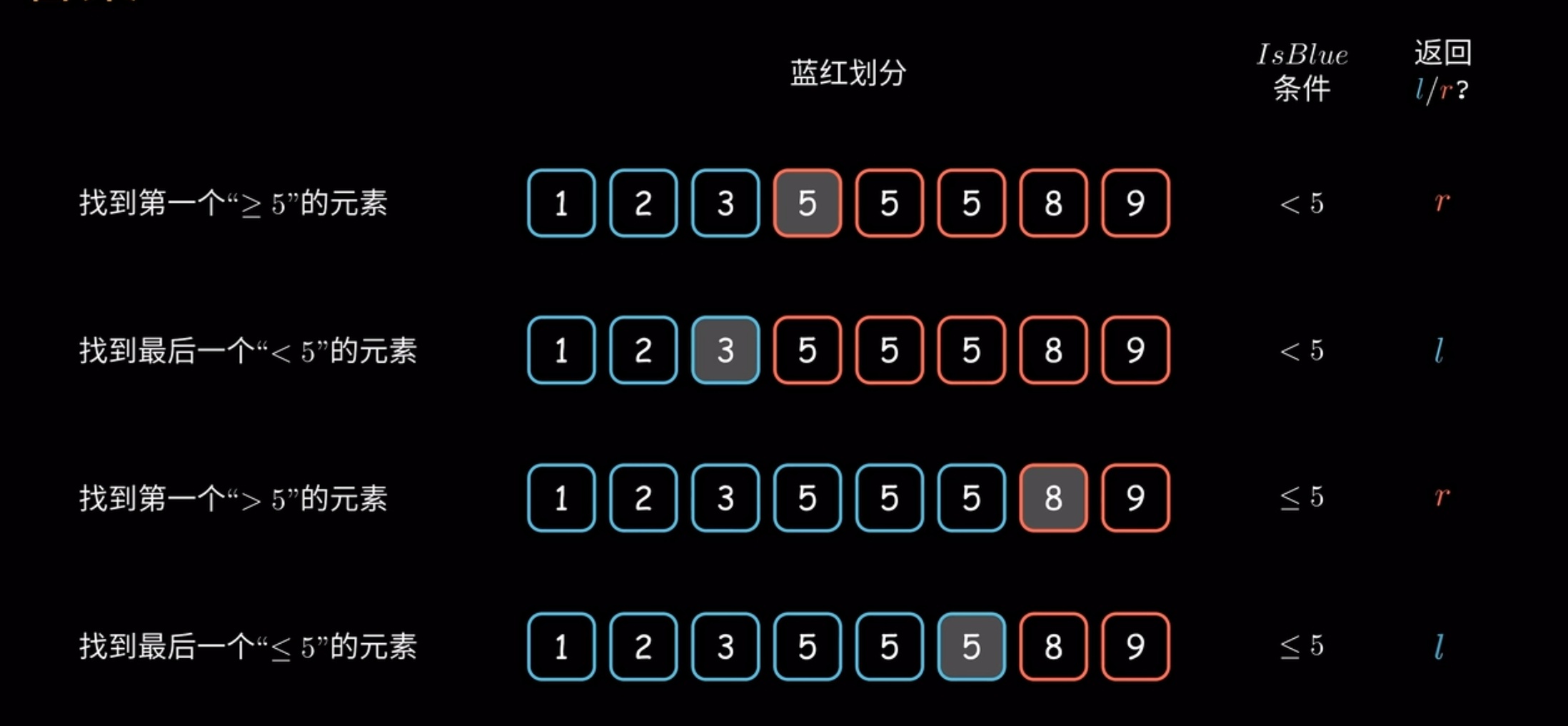
在按照实际情况实现查找功能的时候要判断好IsBlue条件和返回的是l还是r(二分查找和二分答案同一样)。
第五种(STL)
- lower_bound
- 用处:在已排序的范围中查找第一个不小于给定值的元素的位置。
- 返回值:指向第一个不小于给定值的元素的迭代器。
- upper_bound
- 用处:在已排序的范围中查找第一个大于给定值的元素的位置。
- 返回值:指向第一个大于给定值的元素的迭代器。
和第四种方法相对应的四种查找案例(仔细看里面有小黄字)

在二分查找中有的时候可以用,二分答案通常就不行了,乖乖手搓二分。
STL是C++的东西,要打 algorithm 头文件
实数二分说明
学会了整数二分的话这就挺简单的了,自己看看例题依葫芦画瓢一下也就会了(可以参考例题题解,去别的文章或视频学习……),注意一下实数比较的时候要用eps等等就行。
例题
二分查找:P2249 【深基13.例1】查找
二分查找(不用stl和用stl都尝试一遍):P1102 A-B 数对
二分答案:P1873 [COCI 2011/2012 #5] EKO / 砍树
实数二分答案:P1024 [NOIP2001 提高组] 一元三次方程求解
结语
累死了,终于把二分总结完了,快2k字的文章不介意你们稍稍打赏一下,就是1分钱也行啊(^▽^)嘿嘿~


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)