搜索算法讲解

深度优先搜索-DFS

P1219 [USACO1.5] 八皇后 Checker Challenge

一个如下的 $6 \times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

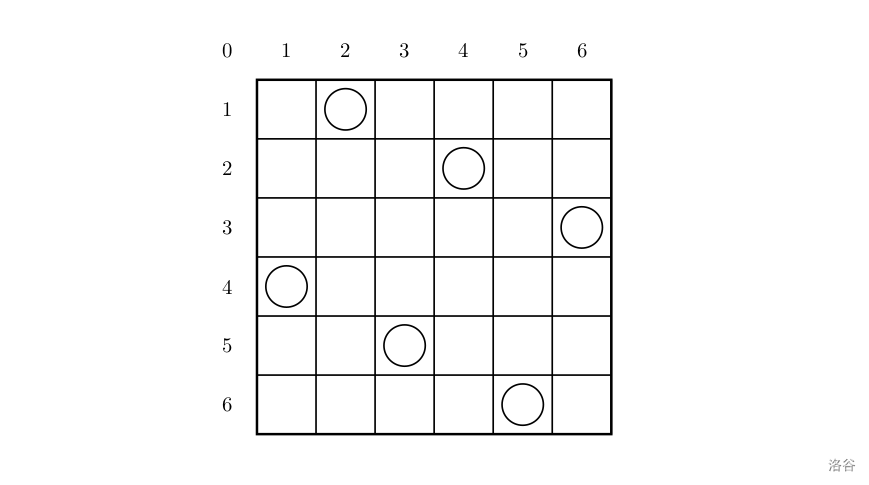
上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $1\ 2\ 3\ 4\ 5\ 6$

列号 $2\ 4\ 6\ 1\ 3\ 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

思路

首先思考暴力枚举解法，注意到每一行只能放一个，那就可以一行一行枚举，然后判断是否合法接口。

然后会发现暴力枚举中有很多不必要的操作，比如说我们枚举到第3行把棋子放在第3列，发现这个位置是非法的，难么其实我们就没有必要再往下面的层去枚举了，应该直接把第3行的棋子放到后面的列继续枚举即可。

总结一下现在的方法：就是一行一行的放棋子，如果在该行放置的棋子是合法的，就继续放下一行的；如果枚举是非法的，就不用继续枚举下一行了，而是更换当前行的棋子。

这种方式称为回溯算法，我们这里使用深度优先搜索来实现。

DFS板子

void dfs(int k) { // k代表递归层数，或者说要填第几个空
	if (所有空已经填完了) {
		// 判断最优解 / 记录答案
		return;
	}
	for (枚举这个空能填的选项) {
		if (这个选项是合法的) {
			占位
			dfs(k + 1) // 下一层递归
			取消占位
		}
	}
}

接下来还有个难点，就是如何判断选项合法。首先行上一定不会冲突，因为我们是一行一行枚举的，每行只能放一个；然后列的话我们可以创建一个名如used_col的bool列表（当然int列表也可以）去存每一行的使用状态，为true就是用过了，就不能再该行再次使用，false就是没用过，就可以在该行使用；然后对角线就比较麻烦，而且对角线有两种，一种是从左往右上升，一种是从左往右下降的，都要判断清楚。

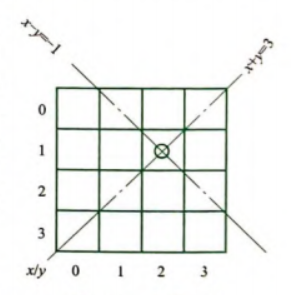
我们可以发现，从左往右上升的对角线上的点有一个特点，就是x+y的值都一样，并且除了该对角线上的点都一定不满足这个条件；另一种对角线则是x-y的值都一样。这样我们就可以开2个数组去记录对角线的使用状态，首先看x+y为定值的对角线，我们就只需要用数组记录这个定值对应的使用情况即可，就是开一个bool数组，定值对应数组下标即可；然后看x-y为定值的对角线，思路和前者相同，但是要注意定值可能为负数，就不能作为数组下标，那么就给定值加上一个较大（比x-y的最小值的绝对值大）的固定的整数再作为数组下标即可。

解题代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N = 100;

LL n, ans = 0;
LL arr[N], used_col[N], used_1[N], used_2[N]; 

void dfs(int k) {
	if (k > n) {
		ans++;
		if (ans <= 3) {
			for (LL i = 1; i <= n; i++) cout << arr[i] << " ";
			cout << endl;
		}
		return;	
	}
	
	for (LL i = 1; i <= n; i++) {
		if (!used_col[i] && !used_1[k + i] && !used_2[k - i + 20]) {
			arr[k] = i, used_col[i] = 1, used_1[k + i] = 1, used_2[k - i + 20] = 1; // 占位
			dfs(k + 1); // 递归下一层
			used_col[i] = 0, used_1[k + i] = 0, used_2[k - i + 20] = 0; // 取消占位
		}
	}
}

int main() {
	cin >> n;
	dfs(1);
	cout << ans;
	
	return 0;
}

广度优先搜索-BFS

深度优先搜索会优先考虑搜索的深度。形象点说，就是不找到一个答案不回头。当答案在整棵解答树中比较稀疏时，深度优先搜索可能会先陷人过深的情况，一时半会儿找不到解。有时候需要解决连通性、最短路问题时，可以考虑使用广度优先搜索。

P1443 马的遍历

有一个 $n \times m$ 的棋盘，在某个点 $(x, y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

思路

这题拿dfs做的话很难写，因为他没有一层一层的体现。这道题适合的方法是bfs。

广度优先搜索会优先考虑每种状态的和初始状态的距离，形象点说，与初始状态越接近的情况会优先考虑。再具体一点：每个时刻要做的事情就是从上个时刻每个状态扩展出新的状态。

(开始在图上模拟)

当输入是 4 4 1 1时，扩展方向如图(a)。

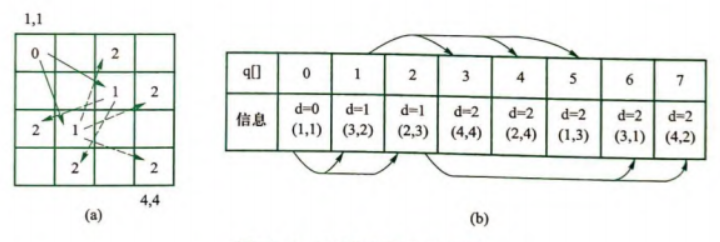
广度优先搜索使用队列实现：先将初始状态加人到空的队列中，然后每次取出队首，找出队首所能转移到的状态，再将其压入队列；如此反复，直到队列为空。这样就能保证一个状态在被访问的时候一定是采用的最短路径。

当输入是4 4 1 1时，队列变化如图(b)。

BFS板子

Q.push(初始状态); // 将初始状态入队
while (!Q.empty()) {
	State u = Q.front(); // 取出队首
	Q.pop(); // 出队
	for (枚举所有可扩展状态) // 找到u的所有可达状态v
		if (是合法的) // v需要满足某些条件，如未访问过、未在队内等
			Q.push(v); // 入队（同时可能需要维护某些信息）
 }

就本题而言，先建立一个结构体数组用于存储扩展的结点。先让起点人队，然后在队列取状态逐个扩展。容易被证明每个点被扩展到时一定是最少步数，这里对应了上面说的与初始状态越接近的情况会优先考虑。又因为每个点只被扩展了一次，所以以复合度是O（mn）。

解题代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

struct coord {
	int x, y;
};

queue<coord> Q; 

LL n, m, x, y, ans[410][410];
LL movee[8][2] = {{2, 1}, {-2, -1}, {1, 2}, {-1, -2}, {2, -1}, {-2, 1}, {-1, 2}, {1, -2}};

int main() {
	memset(ans, -1, sizeof(ans));
	cin >> n >> m >> x >> y;
	ans[x][y] = 0;
	Q.push((coord){x, y});
	while (!Q.empty()) {
		coord u = Q.front();
		LL x = u.x, y = u.y;
		Q.pop();
		for (LL i = 0; i < 8; i++) {
			LL xx = x + movee[i][0], yy = y + movee[i][1];
			if (xx < 1 || xx > n || yy < 1 || yy > m || ans[xx][yy] != -1) continue;
			Q.push((coord){xx, yy});
			ans[xx][yy] = ans[x][y] + 1;
		}
	}
	for (LL i = 1; i <= n; i++, puts("")) {
		for (LL j = 1; j <= m; j++) {
			cout << ans[i][j] << " ";
		}
	}
	
	
	return 0;
}